A comparison of 3 different methods for assessment of skeletal age when treating leg-length discrepancies: an inter- and intra-observer study
Anne Berg BREEN 1, Harald STEEN 1,2, Are PRIPP 3, Ragnhild GUNDERSON 4, Hilde Kristine Sandberg MENTZONI 5, Else MERCKOLL 4, Wajeeha ZAIDI 5, Mikael LAMBERT 5, Ivan HVID 1, and Joachim HORN 1,6
1 Division of Orthopedic Surgery, Oslo University Hospital, Oslo; 2 Biomechanics Lab, Division of Orthopedic Surgery, Oslo University Hospital, Oslo; 3 Oslo Centre of Biostatistics and Epidemiology, University of Oslo; 4 Division of Radiology, Oslo University Hospital, Oslo; 5 Department of Radiology, Akershus University Hospital, Oslo; 6 Institute of Clinical Medicine, University of Oslo, Norway
Background and purpose — Skeletal maturity is a crucial parameter when calculating remaining growth in children. We compared 3 different methods, 2 manual and 1 automated, in the radiological assessment of bone age with respect to precision and systematic difference.
Material and methods — 66 simultaneous examinations of the left hand and left elbow from children treated for leg-length discrepancies were randomly selected for skeletal age assessment. The radiographs were anonymized and assessed twice with at least 3 weeks’ interval according to the Greulich and Pyle (GP) and Sauvegrain (SG) methods by 5 radiologists with different levels of experience. The hand radiographs were also assessed for GP bone age by use of the automated BoneXpert (BX) method for comparison.
Results — The inter-observer intraclass correlation coefficient (ICC) was 0.96 for the GP and 0.98 for the SG method. The inter- and intra-observer standard error of the measurement (SEm) was 0.41 and 0.32 years for the GP method and 0.27 and 0.21 years for the SG method with a significant difference (p < 0.001) between the methods and between the experienced and the less experienced radiologists for both methods (p = 0.003 and p < 0.001). In 25% of the assessments the discrepancy between the GP and the SG method was > 1 year. There was no systematic difference comparing either manual method with the automatic BX method.
Interpretation — With respect to the precision of skeletal age determination, we recommend using the SG method or preferably the automated BX method based on GP assessments in the calculation of remaining growth.
Citation: Acta Orthopaedica 2022; 93: 222–228. DOI http://dx.doi.org/10.2340/17453674.2021.1133.
Copyright: © 2021 The Author(s). This is an Open Access article distributed under the terms of the Creative Commons Attribution-NonCommercial 4.0 International License (https://creativecommons.org/licenses/by-nc/4.0/), allowing third parties to copy and redistribute the material in any medium or format and to remix, transform, and build upon the material for non-commercial purposes, provided proper attribution to the original work.
Submitted: 2021-05-31. Accepted: 2021-12-06. Published: 2022-01-11.
Correspondence: anneb3@ous-hf.no
ABB, HS, and JH designed the study. ABB, RG, HKSM, EM, WZ, and ML collected the data. AP, ABB, and HS analyzed the data. ABB and AP compiled the manuscript draft. HS, RG, HKSM, EM, WZ, ML, IH, AP, and JH ensured the accuracy of the analyses and approved the final version of the manuscript.
Sutharsan Tharmathas is thanked for valuable technical support.
Acta thanks Bjarne Moeller-Madsen and Björn Vogt for help with peer review of this study.
When treating leg-length discrepancies (LLD) in children the calculation of remaining growth is crucial to estimate the correct timing of epiphysiodesis (1). Recent publications conclude that the use of bone age (BA) is a better predictor compared with chronological age (CA) in these calculations (2,3). According to a study by Dimeglio et al. (4) only one-third (28–35%) of such children have a CA equal to the BA (a difference of less than 6 months). Therefore, correct estimation of BA is of importance for the outcome of procedures for growth modulation, both for correction of LLD and for angular correction (5).
Radiological assessment of maturation by BA is commonly done from hand and wrist radiographs (6,7), elbow radiographs (4,8), and pelvic radiographs (9). A study among members of the Society for Pediatric Radiology in the United States found that 97% of radiologists used hand radiographs and the Greulich and Pyle (GP) atlas for BA assessment (10). The main disadvantage with this method is the limited inter- and intra-observer reliability (11), the lack of resolution and precision in the adolescent growth spurt, and the lack of a radiological reference for the bone ages 11.5 and 12.5 years in girls and 14.5 years in boys. Complementary use of the Sauvegrain (SG) method might therefore be recommended during the adolescent growth spurt (4). Canavese et al. (12) compared the simplified olecranon method, a modification of SG’s original method by Dimeglio et al. (4) based solely on the stages of maturation of the olecranon, with Sanders’ digital method, which is based on the radiographical assessment of the metacarpals and fingers in the anteroposterior view (7). Both the studies by Canavese et al. (12) and by Dimeglio et al. (4) conclude that the methods are equally reliable. Other authors have supported the use of more than 1 method to increase the precision when estimating skeletal maturity (13). To reduce the subjective agreement problem when estimating skeletal maturity, Thodberg et al. (14) developed the BoneXpert (BX) program, which is an automated method in determining skeletal maturity, with a precision reported to be 0.16 years (14). Limitations with this method are the restricted availability of the program and the costs for each calculation. When automated methods are not available, the timing of growth-modulating procedures has to rely on manual determination of BA based on either the GP or the SG method, or a combination of the two. However, a certain precision of this manual BA determination is required to avoid substantial under- or overcorrection when treating LLDs.
Growth-modulating procedures are usually done in either the distal femur, the proximal tibia, or in both. The average longitudinal growth per year in these physes is 1.6 cm during adolescence including the prepubertal growth spurt (15,16). Hence, a lack of precision when assessing bone age of ±6 months wouldcorrespond to 0.8 cm growth in bone length, a difference we consider of clinical significance when calculating remaining growth and the optimal timing of epiphysiodesis.
With this study we wanted to compare the manual methods for bone age determination (GP, SG) by examining the precision in terms of correlation and variability, and the inter- and intra-observer reliability among experienced and less experienced radiologists from 2 Norwegian Hospitals. Second, we wanted to examine the systematic difference when comparing the GP and SG assessments with their original assessments (before study was initiated), CA and BX values.
Material and methods
From a local Health Register consisting of patients investigated using the Moseley Straight Line Graph (17) for LLD we identified 440 examinations with both left AP hand and left elbow radiographs exposed simultaneously for skeletal age assessment.
The GP method was originally based on serial radiographs of the left hand and wrist in 999 children in Ohio, USA during the period 1931–1942. The authors found that the sequence of ossification of all the carpals except the scaphoid was relatively constant in both sexes. GP chose the most representative radiograph for each age and provided a standard deviation (SD) of the assessments (6).
The SG method is based on AP and lateral radiographs of the elbow and allows dividing skeletal age into 6-month intervals during the adolescent growth spurt. The 4 ossification centers of the elbow undergo typical changes before and during puberty in the age range 10–13 years in girls and 12–15 years in boys. The method is based on points given for the degree of maturation of each ossification center; the points are added and plotted in a graph that gives the corresponding BA (8).
By computerized random selection 66 examinations from the period 2007–2019 were stratified in 4 sample groups according to the original assessment of skeletal age by GP: < 11 years, 11–12 years, 13–14 years, and > 14 years. 34 female and 32 male assessments in 31 girls and 29 boys were included (Table 1). All patients were followed for LLD with a variety of etiologies (Table 2, see Supplementary data). The anonymized 66 hand radiographs and 66 elbow radiographs only containing information about the patient’s sex were evaluated for skeletal age estimation according to the GP and SG method by 5 independent radiologists at 2 different institutions. For a second analysis the radiographs were randomly reordered, and the BA assessments were repeated after 3–6 weeks. The radiologists had different levels of experience and were classified into highly experienced (2 radiologists working with both methods for 15 years) and less experienced (3 radiologists, with some experience in using 1 or both methods). In addition, we applied the automated bone age estimation by the BX method (14), v3.0.3 (Visiana ApS, Hørsholm, Denmark) for analysis of the 66 hand radiographs.
The BX method consists of 3 layers, where the first layer reconstructs the border of 15 bones from radiographs of the hand. In the second layer the program calculates what the developer calls the “intrinsic bone age” for 13 of the bones. The BA of the bones must be within 2.4 years of the mean BA of all the bones to be accepted. 8 bones is the minimum of bones accepted for the method to generate an intrinsic BA. Finally, the third layer transforms the intrinsic bone age into GP bone age. The first layer was developed from 1,559 images of mainly Danish children and was validated against the GP atlas (14).
Statistics
Data was described with number of observations (%) or mean (SD) as appropriate. We made Bland–Altman plots to describe and evaluate inter- and intra-observer reliability. Both the intraclass correlation coefficient (ICC) and the standard error of the measurement (SEm) with their 95% confidence intervals (CI) in the inter- and intra-observer analysis were estimated using a nested linear mixed-effects model with random intercepts of subject (i.e., patient) and observer (i.e., radiologist). We used SEm to get an estimate in years of how much the assessments vary among different radiologists and by a single radiologist. The observers in the study were considered a random sample from the population of potential observers. The model gives estimates of the between-subject (i.e., patient) SD, between-observer (i.e., radiologist) SD, and the measurement error (i.e., test–retest) SD as outlined by Bartlett and Frost (18).
An ICC value between 0.75 and 0.90 was considered good and > 0.90 excellent reliability (19). For all SEm results we presented the 95% level of confidence interval defined as ±1.96 × SEm. It is the uncertainty interval with on average 95% of the measurements, and the range of reliability around a given BA assessment in the clinic.
We examined whether experience influenced the assessments by assigning the radiologists into 2 groups (experienced and less experienced). Difference in SEm from the GP assessments versus the SG assessments and from experienced versus less experienced was statistically assessed by a Z-test using the estimated standard errors (SE). We assessed the assumption of normal distribution with descriptive statistics and plots and found it satisfactory. The Z-statistic follows a standard normal distribution under the null hypothesis of SEm being equal for experienced and less experienced radiologists.
We compared the systematic difference in the first assessment between the 2 manual methods, the automatic method, and previous assessment using a random-effects model with a subject-specific random intercept. The fixed effect in the model was the different methods and the systematic difference was expressed by the fixed-effect coefficient with 95% confidence interval (CI) and significance level p ≤ 5%.
To study a possible ceiling effect because the SG method has an upper limit of 13 years in girls and 15 years in boys compared with GP, which has an upper limit of 17 and 19 years, respectively, we did a sub-analysis of the SG method and found a minimal reduction of no clinical relevance.
We used STATA/SE 16.1 (StataCorp LLC, College Station, TX, USA) for the statistical analyses.
Ethics, funding, data sharing, and potential conflicts of interest
The study was approved by the institutional review board (case nr. 18/04927) and the research committee at the Department of Radiology and Nuclear Medicine (KRNnr. 1985). No competing interests were declared. No funding has been received. The raw data is available in our repository.
Results
GP method
The ICC was 0.96 (CI 0.95–0.98). The inter-observer SEm was 0.41 (CI –0.40 to 1.22) years, and the intra-observer SEm was 0.32 (–0.31 to 0.95) years. The inter-observer SEm for the experienced radiologists was 0.35 (–0.33 to 1.0) years compared with 0.43 (–0.42 to 1.3) years for the less experienced (Table 3, see Supplementary data). This difference was statistically significant (p = 0.003). Among radiologists the discrepancy was > 1 year in 55% of the assessments in the first test (Table 4).
| Absolute difference GP (years) | 1st | Assessment 2nd | 1st and 2nd |
| All assessments (n = 660) | |||
| ≤ 0.5 | 277 (84) | 279 (85) | 556 (84) |
| > 0.5 to 1.0 | 17 (5) | 21 (6) | 38 (6) |
| > 1.0 to 2.0 | 33 (10) | 28 (8) | 61 (9) |
| > 2.0 | 3 (1) | 2 (1) | 5 (1) |
| Total | 330 | 330 | 660 |
| Variation among 5 radiologists in 66 separate assessments (n = 330) | |||
| ≤ 0.5 | 13 (20) | 15 (23) | 28 (21) |
| > 0.5 to 1.0 | 17 (26) | 21 (32) | 38 (29) |
| > 1.0 to 2.0 | 33 (50) | 28 (42) | 61 (46) |
| > 2.0 | 3 (5) | 2 (3) | 5 (4) |
| Total | 66 | 66 | 1 32 |
SG method
The ICC was 0.98 (CI 0.96–0.98). The inter-observer SEm was 0.27 (–0.27 to 0.81) years, and the intra-observer SEm was 0.21 (–0.20 to 0.62) years. The inter-observer SEm for the experienced radiologist was 0.19 (–0.18 to 0.56) years compared with 0.30 (–0.30 to 0.90) years for the less experienced (p < 0.001) (Table 3, see Supplementary data). Among radiologists the discrepancy was > 1 year in 17% of the assessments in the first test (Table 5).
| Absolute difference SG (years) | Assessment | ||
| 1st | 2nd | 1st and 2nd | |
| All assessments (n = 660) | |||
| ≤ 0.5 | 297 (90) | 300 (91) | 597 (90) |
| > 0.5 to 1.0 | 22 (7) | 21 (6) | 43 (7) |
| > 1.0 to 2.0 | 10 (3) | 9 (3) | 19 (3) |
| > 2.0 | 1 (< 1) | 0 | 1 (< 1) |
| Total | 330 | 330 | 660 |
| Variation among 5 radiologists in 66 separate assessments (n = 330 | |||
| ≤ 0.5 | 33 (50) | 36 (55) | 69 (52) |
| > 0.5 to 1.0 | 22 (33) | 21 (32) | 43 (33) |
| > 1.0 to 2.0 | 10 (15) | 9 (14) | 19 (14) |
| > 2.0 | 1 (2) | 0 | 1 (< 1) |
| Total | 66 | 66 | 132 |
Combined BA
The ICC was 0.98 (CI 0.98–0.99). The inter-observer SEm was 0.23 (–0.23 to 0.69) years, and the intra-observer SEm was 0.20 (–0.18 to 0.58) years. The inter-observer SEm for the experienced radiologist was 0.20 (–0.18 to 0.58) years and 0.25 (0.23 to 0.73) years for the less experienced (p = 0.001) (Table 3, see Supplementary data).
Comparison of the GP and SG method
The ICC was 0.93 (CI 0.91–0.94). Comparing inter-observer SEm for the manual methods and the combined BA there was a significant difference (p < 0.001) for all 3. Evaluating the discrepancy between the 2 manual methods by years we found that 66% (433/660) of the assessments had a discrepancy of > 0.5 year, 25% (161/660) of > 1 year, and 3% (18/660) of > 2 years (Table 6). The variation in BA assessments by the GP method and the SG method for 1 observer is illustrated by a Bland–Altman plot in the Figure.
| Absolute difference between GP and SG (years) | Assessment | ||
| 1st | 2nd | 1st and 2nd | |
| All assessments (n = 660) | |||
| ≤ 0.5 | 111 (34) | 116 (35) | 227 (34) |
| > 0.5 to 1.0 | 139 (42) | 133 (40) | 272 (41) |
| > 1.0 to 2.0 | 68 (21) | 75 (23) | 143 (22) |
| > 2.0 | 12 (4) | 6 (2) | 18 (3) |
| Total | 330 | 330 | 660 |
| Variation among 5 radiologists in 66 separate assessments (n = 330) | |||
| ≤ 0.5 | 22 (33) | 19 (29) | 41 (31) |
| > 0.5 to s 1.0 | 30 (45) | 31 (47) | 61 (46) |
| > 1.0 to s 2.0 | 13 (20) | 15 (23) | 28 (21) |
| > 2.0 | 1 (< 2) | 1 (< 2) | 2 (< 2) |
| Total | 66 | 66 | 1 32 |
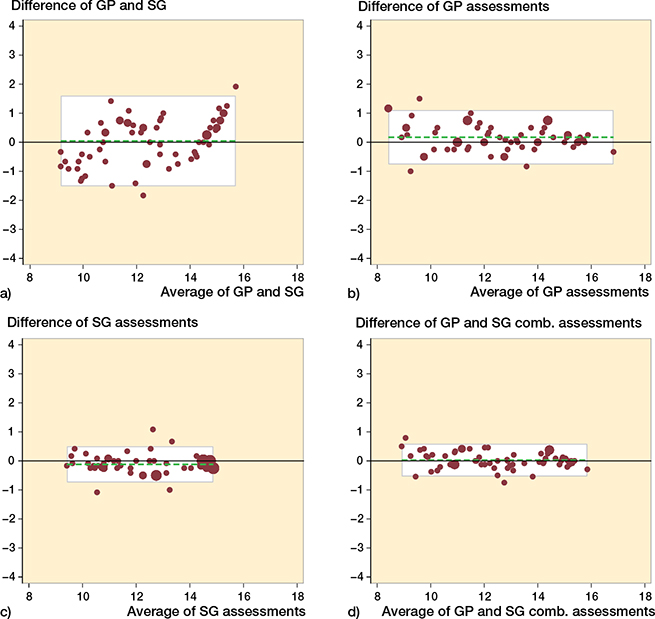
Figure 1. Variation in bone age (BA) assessments by the Greulich and Pyle (GP) and Sauvegrain (SG) methods in our sample of patients (n = 66) illustrated by representative Bland–Altman plots. The white area represents the 95% limits of agreement presented in parentheses. (a) Difference between GP and SG assessments for 1 observer; mean 0.04 (–1.52 to 1.60) years. (b). Difference of GP assessments between 2 observers; mean 0.17 (–0.76 to 1.11) years. (c) Difference of SG assessments between 2 observers; mean –0.12 (–0.74 to 0.50) years. (d) Difference of GP and SG combined assessments between 2 observers; mean 0.03 (–0.54 to 0.59) years.
Systematic difference
There was no statistically significant difference when comparing the GP and SG method and the combined BA with BX. The original GP assessment was different from the new GP assessment (p = 0.01), and from BX (p = 0.05). The original SG assessment was not significantly different compared with the new assessment (p = 0.09).
CA was significantly different compared with both manual BA methods (Table 7).
Discussion
The ICC was > 0.90 and graded as excellent (19) in both the inter- and intra-observer analysis, which corresponds to the findings by Dimeglio et al. (4) and Canavese et al. (12). The ICC however is dependent on the sample’s variation of measurements—a great variation with the same inaccuracy results in a high ICC. Hence, in our opinion the SEm with its 95% confidence that we used is a more useful and clinically relevant description of the precision of BA assessments, which adds a novel insight.
The inter- and intra-observer reliability in this study is significantly better with the SG method than with the GP method in comparing SEm for both. When radiologists perform a BA assessment according to GP, we found a CI level in SEm corresponding to ±0.81 years (i.e., ±10 months). 10 months corresponds to 1.3 cm growth around the knee using the White–Menelaus method. If the same radiologist repeated the GP assessment the CI level was ±0.63 years (i.e., ±7.5 months). For the SG method the CI level was ±0.54 years (i.e., ±6.5 months), corresponding to 0.9 cm growth around the knee using the White–Menelaus method. For the SG method the repeated CI level was ±0.41 years (i.e., ±5 months).
This data shows that precision increases with the second assessment, when 2 BA methods are combined, and with the radiologist’s level of experience. By use of the combined mean BA value a more precise assessment is expected and might favor application of both methods. However, a combination does not consider which method is the most accurate in estimating the true skeletal maturity by BA when there is a clinically significant discrepancy between the 2 assessments. The combination of these 2 methods also requires 3 radiographs, which increases the total amount of radiation of the child.
We found the variation among the 5 radiologists for the first assessment of GP to be > 1 year in 55% of the ratings. This is almost identical with the findings of Cundy et al. (11). The corresponding number of SG assessments was 17%, which underlines the difference in precision between the 2 methods.
Furthermore, our study shows that one-quarter of the assessments had > 1 year discrepancy between the GP and the SG rating. In a clinical setting when treating LLD, a BA assessment that differs by 1 year corresponds to a difference in growth of 0.64 cm in the proximal tibia and 0.95 cm in the distal femur, i.e., a combined 1.6 cm according to the White–Menelaus method (15,16). The mean LLD at the time of epiphysiodesis was 3.7 cm and 2.0 cm at maturity in a recent study by Makarov et al. (2), corresponding to a mean correction of 1.7 cm. A discrepancy between different BA methods > 1 year can therefore be considered clinically significant in the timing of epiphysiodesis.
With a discrepancy > 6 months the use of a combined BA increases the age precision according to our results, but we are not able to conclude whether this also increases the accuracy in terms of the true skeletal maturity, which is a limitation of this study. Another limitation considering the comparison of the manual BA methods is that we compare only the difference in assessments among 5 persons and hence not a real selection from a population, nor was the precision of the GP assessments within different age groups assessed, as the GP atlas lacks pictures of certain ages. We used the mean value of the first assessment by the 5 radiologists when comparing the 2 manual BA methods with the original assessments (which most often were based on 2 assessments by 2 radiologists). This might have increased the precision in the new ratings and favored the results from the current study.
While a statistically significant difference was found when comparing BA from the original GP assessments with the new GP assessments and with BX, no significant systematic difference was found when comparing the original SG assessments with the new SG assessments. In this study the radiographs were anonymized. This eliminates the risk of bias from the radiologist knowing the CA of the patients and former assessments of BA in the same patient. It has been shown that knowing the patient’s CA may cause bias in the GP evaluation (20).The better precision and the comparable results for the original and new SG assessments compared with GP for both the experienced and inexperienced radiologists might be explained by a more objective approach with the SG method.
Considering BX as a reference value, the test for systematic difference comparing BX with the different manual BA methods did not reveal any statistically significant difference versus BX. However, a significant systematic difference was found when comparing both manual methods with CA.
Van Rijn et al. (20) found that the BA based on BX analysis (derived from GP) was on average 0.28 and 0.20 years behind the CA for boys and girls, respectively. In our study this difference was similar: –0.25 years independent of sex. Hence, the maturation profile in our population may be comparable to the Dutch population and representative of modern Western European children.
Conclusion
The SG method is more precise than the GP method, with an uncertainty of ±6 months with the SG method compared with ±10 months with the GP method when a single BA assessment is performed by independent radiologists. Hence, if only manual methods for BA assessments are available, we recommend the SG method in the calculation of remaining growth. Experience reduces the uncertainty in the assessments by 1–2 months and the combination of 2 methods increases the precision by 1 month compared with using SG alone. The increase in precision using 2 methods is minimal in a clinical setting, and we would not recommend using 2 methods because of the added radiation exposure.
We find no systematic difference when comparing the 2 manual BA methods with the automated BoneXpert method. We therefore recommend using BoneXpert if available, to avoid a reduction in precision using manual methods.
- Lee S C, Shim J S, Seo S W, Lim K S, Ko K R. The accuracy of current methods in determining the timing of epiphysiodesis. Bone Joint J 2013; 95-b(7): 993-1000. doi: 10.1302/0301-620x.95b7.30803.
- Makarov M R, Jackson T J, Smith C M, Jo C H, Birch J G. Timing of epiphysiodesis to correct leg-length discrepancy: a comparison of prediction methods. J Bone Joint Surg Am 2018; 100(14): 1217-22. doi: 10.2106/jbjs.17.01380.
- Birch J G, Makarov M A, Jackson T J, Jo C H. Comparison of Anderson–Green growth-remaining graphs and White–Menelaus predictions of growth remaining in the distal femoral and proximal tibial physes. J Bone Joint Surg Am 2019; 101(11): 1016-22. doi: 10.2106/jbjs.18.01226.
- Dimeglio A, Charles Y P, Daures J P, de Rosa V, Kabore B. Accuracyof the Sauvegrain method in determining skeletal age during puberty. J Bone Joint Surg Am 2005; 87(8): 1689-96. doi: 10.2106/jbjs.d.02418.
- Farr S, Alrabai H M, Meizer E, Ganger R, Radler C. Rebound of frontal plane malalignment after tension band plating. J Pediatr Orthop 2018; 38(7): 365-9. doi: 10.1097/bpo.0000000000000846.
- Greulich W W, Idell Pyle S. Radiographic atlas of skeletal development of the hand and the wrist. Stanford, CA: Stanford University Press; 1959.
- Sanders J O, Khoury J G, Kishan S, Browne R H, Mooney J F 3rd, Arnold K D, et al. Predicting scoliosis progression from skeletal maturity: a simplified classification during adolescence. J Bone Joint Surg Am 2008; 90(3): 540-53. doi: 10.2106/jbjs.G.00004.
- Sauvegrain J, Nahum H, Bronstein H. [Study of bone maturation of the elbow]. Annales de radiologie 1962; 5: 542-50.
- Risser J C. The classic: The iliac apophysis: an invaluable sign in the management of scoliosis. Clin Orthop Relat Res 2010; 468(3): 646-53.
- Breen M A, Tsai A, Stamm A, Kleinman P K. Bone age assessment practices in infants and older children among Society for Pediatric Radiology members. Pediatr Radiol 2016; 46(9): 1269-74. doi: 10.1007/s00247-016-3618-7.
- Cundy P, Paterson D, Morris L, Foster B. Skeletal age estimation in leg length discrepancy. J Pediatr Orthop 1988; 8(5): 513-5.
- Canavese F, Charles Y P, Dimeglio A, Schuller S, Rousset M,Samba A, et al. A comparison of the simplified olecranon and digital methods of assessment of skeletal maturity during the pubertal growthspurt. Bone Joint J 2014; 96-b(11): 1556-60. doi: 10.1302/0301620x.96b11.33995.
- Journeau P. Update on guided growth concepts around the knee in children. Orthop Traumatol Surg Res 2020; 106(1s): S171-s80. doi: 10.1016/j.otsr.2019.04.025.
- Thodberg H H, Kreiborg S, Juul A, Pedersen K D. The BoneXpert method for automated determination of skeletal maturity. IEEE Trans Med Imaging 2009; 28(1): 52-66. doi: 10.1109/tmi.2008.926067.
- White J W, Stubbins S G. Growth arrest for equalizing leg lengths. JAMA 1944; 126(18): 1146.
- Menelaus M B. Correction of leg length discrepancy by epiphysial arrest. J Bone Joint Surg Br 1966; 48(2): 336-9.
- Moseley C F. A straight-line graph for leg-length discrepancies. J Bone Joint Surg Am 1977; 59(2): 174-9.
- Bartlett J W, Frost C. Reliability, repeatability and reproducibility: analysis of measurement errors in continuous variables. Ultrasound Obstet Gynecol 2008; 31(4): 466-75. doi: 10.1002/uog.5256.
- Koo T K, Li M Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J Chiropr Med 2016; 15(2): 155-63. doi: 10.1016/j.jcm.2016.02.012.
- van Rijn R R, Lequin M H, Thodberg H H. Automatic determination of Greulich and Pyle bone age in healthy Dutch children. Pediatr Radiol 2009; 39(6): 591-7. doi: 10.1007/s00247-008-1090-8.
Supplementary data